The Grid

  Fig. 1 The Portal Grid is constructed inside this rectangle. It is one of three identical rectangles found in the hexagon that make up the 6-pointed star. The grid is composed of a fanlike array of ‘angles of ascension’, or rays, spaced 15 degrees apart. The earth’s rotational rate of spin on it’s axis is 15 degrees per hour. It seems likely that the ancients used this geometry, or trigonometry, to measure time. This geometry most probably also became the model for suggesting a 24-hour day, which is actually 23 hours and 56 minutes.

When analyzing particular ancient art, motifs implying the square root of three relevant to the narrative will be located in relation to certain design elements. Any two objects in a corner-to-corner relationship, on either of the long sides of this rectangle, are in a square root of three relationship. The corners of this rectangle, as well as the other hexagon chords, are where the arcs and chords meet on the circle’s circumference. This creates a space between them, a ‘gap’, or ‘pocket’ where certain objects appear to have been designed to fit. Any hands, eyes, or other prominent objects located on the long sides are something to watch when scrolling.

Fig. 2 The first step is to determine the centers of each of the two long sides of the rectangle. A line connecting the top and bottom points of the hexagon simply and accurately divides these sides in half further establishing the x/y axis origin from which the rays are projected.

Fig.3 To establish the center of the short sides requires an arc the width of the radius of the originating circle and, or the length of the short side, same thing. By swinging a compass with it’s point located at the center of either long side, the arc just ‘tangents’ the center of the opposing long side and ends at the center of either short side.

Fig. 4Repeating the same arc opposite approximates the Christian fish, and appears to be an arc of a covenant, the long side always being a multiple of the square root of three. See,‘The Square Root of Three’ below.

In Solomon’s temple, ‘The inner sanctuary he prepared in the innermost part of the house, to set there the ark of the covenant of the Lord. The inner sanctuary was twenty cubits long, twenty cubits wide, and twenty cubits high. 1 Kings 6/19-20.

This 20x20x20 sanctuary is a cube. The diagonal of a cube is the square root of three. The ‘ark’ may very well be an ‘arc’, one associated with either of the two triangles formed by the diagonals, the long sides of which are always a multiple of the square root of three as shown in Fig. 7.

Noah’s Ark may also be an ‘arc’, one that encodes the mathematics found by applying the Pythagorean Theorem to the 3/4/5 Pythagorean Right Triangle, shown in Fig. 7. This also includes a direct reference to the Fibonacci Series. The ark is 300 cubits long, 50 cubits wide, and 30 cubits tall. Note the width of 50, divided by height of 30 equals 1.6666666. This is the first of the Fibonacci Series, 5/3 = 1.6666666.

Length/Height; 300/30 = 10

Length/Width; 300/50 = 6

10/6 = 1.66666666

Width/Height; 50/30 = 1.66666666

[l/h] / [l/w] x [w/h] = 2.7777777 (1.666666662)

The hypotenuse of the 3/4/5 right triangle is 25, (52). The hypotenuse of 25 divided by the base of 9, (32) = 2.7777777.

The ‘ark of the covenant’ may be encoding the Pythagorean Theorem, a2+b2 = c2, the square root of three, and the Fibonacci Series. ‘Noah’s Ark’ may likewise be encoding the Pythagorean Theorem and the 3/4/5 right triangle.

  Fig. 5 Determining the 15-degree angle intervals of the rays begins with a hexagon and the 6-pointed star. The circles at either end of the rectangle are located at the centers of the short sides and tangent two sides of the 6-pointed star, as shown. The centers of these circles and short sides, located by the arc described above, establish the 30-degree rays projected from the x/y origin located at the center point of the lower long side. The 15-degree and 45-degree rays projected from the same point tangent the circle on the low and high sides respectively. The 60-degree ray is established at the intersection of two arcs drawn with centers at either corner and the center of the long side. The 75-degree ray tangents a circle with it’s center located at the center point of the upper long side. This circle tangents the sides of the 6-pointed star similarly to the other two circles, but from the inside of the upper 60-degree equilateral triangle of the star. The 90-degree ray, not shown, is the original line drawn to establish the centers of the long sides.

Fig. 6 Projecting this array from above with the 90-degree y-axis included, completes the ‘Portal Grid’.

LXI. Angels go off to measure Paradise:

LXI. 1. And I saw in those days how long cords were given to those

angels, and they took to themselves wings and flew, and they went towards the north.

2. And I asked the angel, saying unto him; ‘Why have those (angels)

taken these cords and gone off?’ And he said to me; ‘They have gone to measure.’

3.And the angel who went with me said unto me;

These shall bring the measures of the righteous,

And the ropes of the righteous to the righteous,

That they may stay themselves on the name of

The Lord of Spirits forever and ever.

THE BOOK OF ENOCH, R.H.Charles, Dover Publications 2007, p79

Fig. 7 This circle drawn in the center of the rectangle intersects all of the angle pairs where they meet at 90-degree angles. i.e. 15/75, 30/60, 45/45, 60/30, and 75/15. The 45/45 pair meeting the circle at the centerline proves to be quite a significant alignment, as shown below. The circle’s diameter is equal to the short side of the rectangle, making it one half the size of the originating circle. Repeating the ‘acts of creation’ with this new circle ad infinitum, like the 6-pointed star and the Hexagon, creates a sort of self perpetuating portal of ever smaller dimensions around an ‘empty center’. This empty space is further dimensionally reduced in the center of the Portal Grid where there are no angle pairs meeting at the centerline, only the single 90 degree y-axis. This area is formed by the four 75-degree rays projected from below and above. It corresponds to 12 noon and possibly references the zenith passage of the sun. Because of the tilt in the earth’s polar axis, the zenith sun passes directly overhead at noon, ‘casting no shadows’. This phenomena only occurs within the tropics, 23.4 degrees north or south of the equator. Is this the Valley of the Shadow of Death? Is the 75 degree ray projected from above just past the valley of death the ‘right hand of god’? This 75 degree ray may more properly be referred to as the ray at 115 degrees, but the magical math of the angle pairs and their meeting the circle at right angles disappears. This area is the ‘crossing’, if there is one.

THE EMERALD TABLET OF HERMES

0) Here (is) that which the priest Sagjus of Nabulus has dictated concerning the entrance of Balinas into the hidden chamber…After my entrance into the chamber, where the talisman is set up, I came upon an old man sitting on a golden throne, who was holding an emerald in one hand.

And behold the following-in Syriac, the primordial language-was written theron;

1) Here (is) a true explanation, concerning which there can be no doubt.

2) It attests; The above from the below, and the below from the above-the work of the miracle of the One.

3) And things have been from this principle substance through a single act. How wonderful is this work! It is the main (principle) of the world and is it’s maintainer.

Arabic Version from the German of Ruska

From Idres Shah

1) The truth, certainty, truest, without untruth.

2) What is above is like what is below. What is below is like what is above. The miracle of unity is to be attained.

3) Everything is formed from the contemplation of unity, and all things come about from unity, by means of adaptation.

The Emerald Tablet of Hermes Kessinger Publications, pp 4,14,15

The Square Root of Three

Fig. 8 The diagonal of the square equals the diameter of the enclosing circle. The centers of both occur at the origin of an x/y axis projected upon a grid of squares with sides of 1. The origin is located at the common corner of the four squares that surround the center. The sides of the ‘square in the circle’ are each diagonals of the squares of the grid. The diagonal of a square with sides of 1 is the square root of two, making the diagonal of the square in the circle the square root of two, squared, which equals 2.This also makes the diameter of the circle 2, the radius, 1.

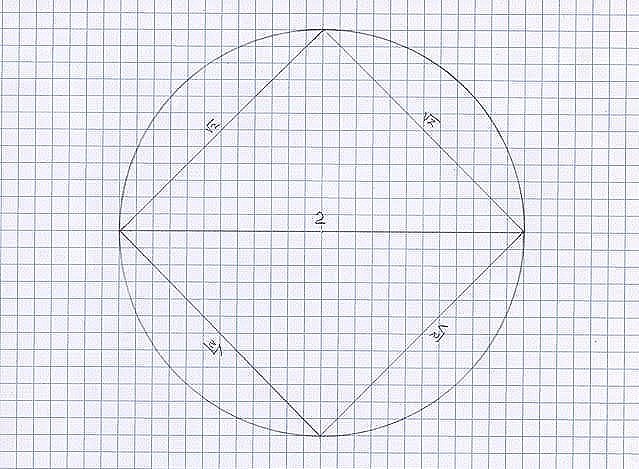
  Fig. 9 The two diagonals of this rectangle create a pair of 60/60/60-degree equilateral triangles. Removing one of the diagonals leaves a 30-60-90-degree right triangle to which we can apply the a2+b2=c2 Pythagorean Theorem. ‘a’, the short side, equals 1,being the same as the radius of the circle in Fig.6 with a diameter of 2, and knowing the length of ‘c’, the hypotenuse is 2, because it is the diameter of the circle we have the following;

a2+b2=c2

12+b2=22

4-1=3

b2 = (square root of three)2

b = square root of three

As mentioned above, the diagonal of the cube, the three-dimensional shape enclosed in a sphere, is the square root of three, and by extension, the earth being a sphere, it’s polar axis, could also be considered the square root of three. How relevant the square root of three is to celestial navigation or accurately determining the circumference of the earth using the polar axis is, I don’t know. The square root of three does seem encoded as a particular mathematical constant and what exactly was understood, or intended by different cultures may be entirely different, or exactly the same, both deriving from the same source, the circle. The ‘quincunx’ motif found in Mesoamerica and first seen in Olmec art may very well derive from this geometry if these rectangles and their diagonals enclose true equilateral triangles, which they appear to do. But how much knowledge about the rest of the mathematics involved and the square root of three is implied by these diagonals locating the ‘center’ of this rectangle, the same center it shares with the cube. That use of this motif certainly implies a more profound knowledge and by necessity revisits the issue of who the Olmec really were and what they possibly knew.

Fig. 10 This diamond shape is composed of two back to back, 60-60-60 equilateral triangles whose apexes occur at the centers of the short sides and are formed by the four 30-degree rays projected from the centers of the long sides. Though not really back to back, unless a 90-degree y-axis is added recreating another 60-60-60-degree mathematical constant, this shape could be the basis, or reference to one of the oldest symbols, and that is the ‘diamond shaped net’, whose diamond sections differ from those nets with square sections. This symbol is taken up in more detail in the section ‘ART MOTIFS’

 Fig. 11 ‘The Bucket’ The two concentric circles that tangent the 45-degree rays and intersect the angle pairs at 90 degrees, imply the ecliptic, the sky overhead, and act as handles for certain objects that further suggest a specific body of knowledge. The Neo- Assyrian ‘bucket’s’ squared bottom of approximately 900-700 BCE, is identical to the one seen in Monument 19 from La Venta, ca.900 BCE. This Olmec carving is the first known representation of the ‘Feathered Serpent’ in Mesoamerica and coupled with the ‘bucket’ directly links whatever esoteric knowledge they share. No other art motifs, or objects like these with round handles found in Mesoamerica have squared bottoms. Teotihuacan and Mayan examples have local variations for these bottom portions that seem to mimic their local geography above or below the Isthmus of Tehuantepec.

Fig.12 ‘Olmec Eye’? Fig.15

Fig.13 ‘Grail Cup’? If so, does this make the ‘Portal Grid’, the ‘Holy Grail’?